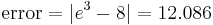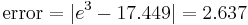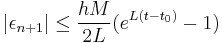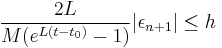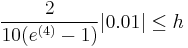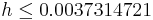Euler method
In mathematics and computational science, the Euler method, named after Leonhard Euler, is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic kind of explicit method for numerical integration of ordinary differential equations and is the simplest kind of Runge-Kutta method.
Contents |
Informal geometrical description
Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slope of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.
The idea is that while the curve is initially unknown, its starting point, which we denote by  is known (see the picture on top right). Then, from the differential equation, the slope to the curve at
is known (see the picture on top right). Then, from the differential equation, the slope to the curve at  can be computed, and so, the tangent line.
can be computed, and so, the tangent line.
Take a small step along that tangent line up to a point 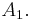 If we pretend that
If we pretend that 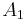 is still on the curve, the same reasoning as for the point
is still on the curve, the same reasoning as for the point 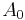 above can be used. After several steps, a polygonal curve
above can be used. After several steps, a polygonal curve 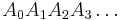 is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite (although things are more complicated for stiff equations, as discussed below).
is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite (although things are more complicated for stiff equations, as discussed below).
Derivation
We want to approximate the solution of the initial value problem
by using the first two terms of the Taylor expansion of y, which represents the linear approximation around the point (t0,y(t0)) . One step of the Euler method from tn to tn+1 = tn + h is
The Euler method is explicit, i.e. the solution 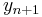 is an explicit function of
is an explicit function of 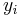 for
for 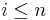 .
.
While the Euler method integrates a first order ODE, any ODE of order N can be represented as a first-order ODE: to treat the equation
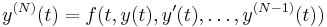 ,
,
we introduce auxiliary variables 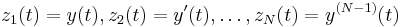 and obtain the equivalent equation
and obtain the equivalent equation
This is a first-order system in the variable 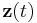 and can be handled by Euler's method or, in fact, any other scheme for first-order systems.
and can be handled by Euler's method or, in fact, any other scheme for first-order systems.
Example
Given the differential equation 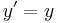 and the initial point
and the initial point 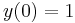 , we would like to use the Euler method to approximate
, we would like to use the Euler method to approximate 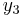 using step size
using step size 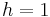 .
.
The Euler method is
so first we must compute 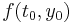 . This simple differential equation depends only on
. This simple differential equation depends only on  , so we need only worry about inputting the values for
, so we need only worry about inputting the values for  .
.
By doing the above step, we have found the slope of the line that is tangent to the solution curve at the point 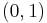 . Recall that the slope is defined as the change in
. Recall that the slope is defined as the change in  divided by the change in
divided by the change in  , or
, or 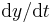 .
.
The next step is to multiply the above value by the step size  .
.
Since the step size is the change in  , when we multiply the step size and the slope of the tangent, we get a change in
, when we multiply the step size and the slope of the tangent, we get a change in  value. This value is then added to the initial
value. This value is then added to the initial  value to obtain the next value to be used for computations.
value to obtain the next value to be used for computations.
The above steps should be repeated to find 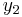 and
and 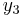 .
.
Due to the repetitive nature of this algorithm, it can be helpful to organize computations in a chart form, as seen below, to avoid making errors.
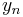 |
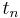 |
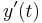 |
 |
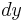 |
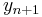 |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 2 |
| 2 | 1 | 2 | 1 | 2 | 4 |
| 4 | 2 | 4 | 1 | 4 | 8 |
Error
The magnitude of the errors arising from the Euler method can be demonstrated by comparison with a Taylor expansion of y. If we assume that 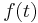 and
and 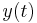 are known exactly at a time
are known exactly at a time 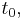 then the Euler method gives the approximate solution at time
then the Euler method gives the approximate solution at time 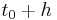 as:
as:
In comparison, the Taylor expansion in  about
about 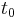 gives:
gives:
Since we know that 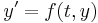 it follows that
it follows that
This, along with 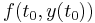 can be inserted into the Taylor expansion in
can be inserted into the Taylor expansion in  about
about 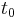 .
.
The error introduced by the Euler method is given by the difference between these equations:
For small  , the dominant error per step, or the local truncation error, is proportional to
, the dominant error per step, or the local truncation error, is proportional to 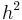 . To solve the problem over a given range of
. To solve the problem over a given range of  , the number of steps needed is proportional to
, the number of steps needed is proportional to 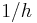 so it is to be expected that the total error at the end of the fixed time, or the global truncation error, will be proportional to
so it is to be expected that the total error at the end of the fixed time, or the global truncation error, will be proportional to  (error per step times number of steps). Because the global truncation error is proportional to
(error per step times number of steps). Because the global truncation error is proportional to  , the Euler method is said to be first order. This makes the Euler method less accurate (for small
, the Euler method is said to be first order. This makes the Euler method less accurate (for small  ) than other higher-order techniques such as Runge-Kutta methods and linear multistep methods.
) than other higher-order techniques such as Runge-Kutta methods and linear multistep methods.
As stated in the introduction, decreasing the step size can help to make the approximation more accurate and decrease the error between the two curves. The error to three decimal places for the example in the above section (with step size 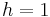 )is the following:
)is the following:
When the step size is changed to 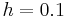 our
our 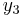 value becomes
value becomes 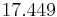 . The error, then, for step size
. The error, then, for step size 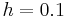 is the following:
is the following:
Although the error has decreased, our approximation is still not particularly accurate. In addition, since the step size decreased with no change in the interval, the number of iterations has increased to thirty. While possible, it is no longer reasonable to do these computations by hand.
Error bound
As with other methods, there is a way for us to determine an error bound for a particular problem. The error bound on the global error is given by[1]:
where  is the step size,
is the step size,  is the upper bound on the second derivative of
is the upper bound on the second derivative of  on the given interval (which must be estimated), and
on the given interval (which must be estimated), and  is the Lipschitz constant.
is the Lipschitz constant.
If the error bound is computed, it can be seen, once again, that if small error is desired, the step size  must be very small.
must be very small.
For instance, let us calculate the step size required for global truncation error to be 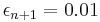 , assuming a maximum value for the second derivative of
, assuming a maximum value for the second derivative of 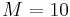 , a Lipschitz constant of
, a Lipschitz constant of 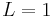 , and
, and  from zero to four. Using the equation given, we obtain the following:
from zero to four. Using the equation given, we obtain the following:
which means that h must be smaller than the above to get the desired error or less, and 4/h, or about 1072 iterations will need to be completed to do so. The large number of steps, and thus high computation cost, supports the use of alternative, higher-order methods such as Runge–Kutta methods or linear multistep methods.
Numerical stability
The Euler method can also be numerically unstable, especially for stiff equations. This limitation—along with its slow convergence of error with h—means that the Euler method is not often used, except as a simple example of numerical integration. The instability can be avoided by using the Euler–Cromer algorithm.
See also
- Numerical integration of ordinary differential equations
- For numerical methods for calculating definite integrals, see Numerical integration
- Gradient descent similarly uses finite steps, here to find minima of functions
- Dynamic errors of numerical methods of ODE discretization
References
- Ascher, Uri M.; Petzold, Linda Ruth. Computer methods for ordinary differential equations and differential-algebraic equations. 1998. SIAM. ISBN 0898714125
External links
|
|||||||||||

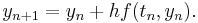
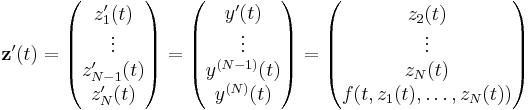
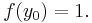
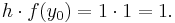
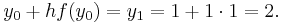
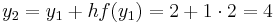
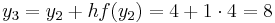
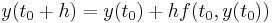
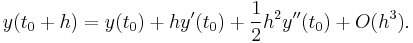
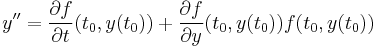
![y(t_0 %2B h) = y(t_0) %2B h f(t_0, y(t_0)) %2B \frac{1}{2}h^2[{\partial f\over\partial t}(t_0, y(t_0)) %2B {\partial f\over\partial y}(t_0, y(t_0)) f(t_0, y(t_0))] %2B O(h^3).](/2012-wikipedia_en_all_nopic_01_2012/I/fa1b40028862483e80dc977bba278591.png)
![\frac{1}{2}h^2 [{\partial f\over\partial t}(t_0, y(t_0)) %2B {\partial f\over\partial y}(t_0, y(t_0)) f(t_0, y(t_0))] %2B O(h^3).](/2012-wikipedia_en_all_nopic_01_2012/I/f8fe9d9c702b709788d33d08e2e74d1d.png)